Leetcode - Algorithm - Divide Two Integers

    |     algorithm leetcode math binary search   |    

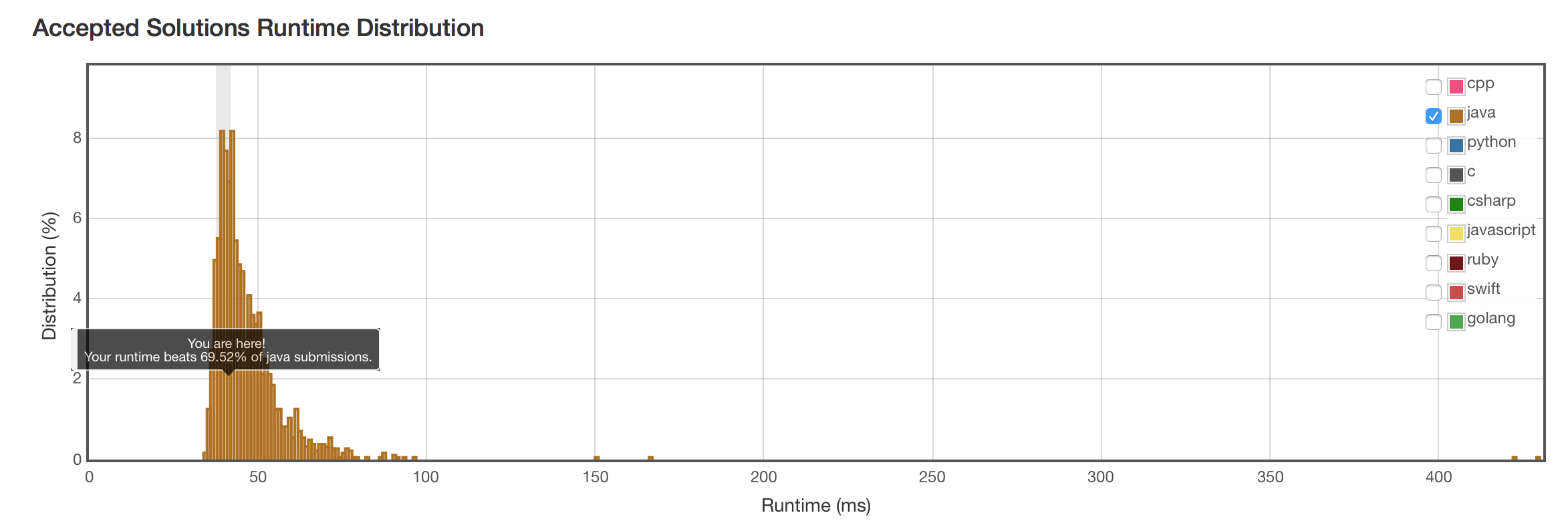
题目

Divide two integers without using multiplication, division and mod operator.

If it is overflow, return MAX_INT.

暴力减法

不让用乘法除法，就在dividend上，不断地减去divisor。

这题先要先处理3个edge case:

  1. 0不能当除数
  2. 0除以任何数等于0
  3. int不能表示2147483648,所以-2147483648/-1会溢出。

第二个关键，在于处理正负号，否则负数的情况将面对2的补码，就会非常复杂。所以先用Integer.signum()函数处理好结果的正负号，然后所有计算都在正数的范畴进行。

代码

public class Solution {
    public int divide(int dividend, int divisor) {
        if (divisor == 0) { return Integer.MAX_VALUE; } // 0不能当除数
        if (dividend == Integer.MIN_VALUE && divisor == -1) { return Integer.MAX_VALUE; } // int不能表示2147483648
        if (dividend == 0) { return 0; } // 0除以任何数等于0
        int sign = (Integer.signum(dividend)== Integer.signum(divisor))? 1:-1; // get the sign
        int dividendAbs = Math.abs(dividend);
        int divisorAbs = Math.abs(divisor);
        int times = 0;
        while (true) {
            dividendAbs = dividendAbs - divisorAbs;
            if (dividendAbs >= 0) {
                times++;
            } else {
                break;
            }
        }
        return (sign==1)? times : -times;
    }
}

结果

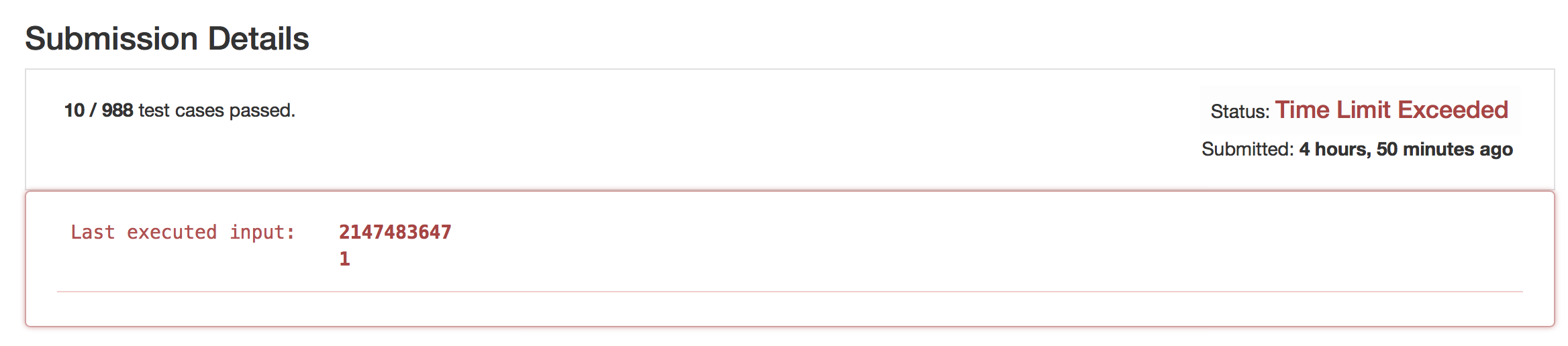
效率非常差，果然在最坏情况卡住了。2147483647/1就要做2147483647次减法。 devide-two-integers-1

用位移操作

举例来说，比如被除数是110，除数是10，

把10不断乘以2，来逼近被除数110。结果最多可以左移3位，说明110至少是10的8倍。

10 << 0 == 10  < 110
10 << 1 == 20  < 110
10 << 2 == 40  < 110
10 << 3 == 80  < 110
-------------------------- 停住
10 << 4 == 160 > 110

110 - 10 << 3 = 30
result = result + 1 << 3 = 8

扣掉之前的80，剩下30，继续上面的过程，

10 << 0 == 10  < 30
10 << 1 == 20  < 30
-------------------------- 停住
10 << 2 == 40  > 30

30 - 10 << 1 = 10
result = result + 1 << 1 = 8 + 2 = 10

直到最后被除数剩下的余数小于除数10。

10 << 0 == 10  == 10
-------------------------- 停住
10 << 1 == 20  > 10

10 - 10 << 0 = 0
result = result + 1 << 0 = 10 + 1 = 11

edge case和符号处理这两个简化问题的手段，和第一种方法相同。

代码

public class Solution {
    public int divide(int dividend, int divisor) {
        // edge case
        if (divisor == 0) { return Integer.MAX_VALUE; } // 0不能当除数
        if (dividend == Integer.MIN_VALUE && divisor == -1) { return Integer.MAX_VALUE; } // int不能表示2147483648
        if (dividend == 0) { return 0; } // 0除以任何数等于0
        // treat sign
        int sign = (Integer.signum(dividend)== Integer.signum(divisor))? 1:-1; // get the sign
        // division
        int result = 0;
        long dividendL = Math.abs((long)dividend), divisorL = Math.abs((long)divisor);
        while (dividendL >= divisorL) {
            int shift = 1;
            while (dividendL >= (divisorL << shift)) { shift++; }
            result += 1 << (shift-1);
            dividendL -= (divisorL << shift-1);
        }
        return (sign == 1)? result : -result;
    }
}

结果

银弹！ devide-two-integers-2